여러분은 5주차 강의에서 4주차 강의에 이어서 다소 복잡한 선택 구조로 if-else 체인 구조, 중첩 if 문, switch 문 등에 대해서 다루었다. 여기서는 이러한 다양한 선택 구조를 사용 가능한 프로그램 예제를 살펴본다.

| 분석 | ||||||||||||||||||
|
여러분은 이미 주어진 2차방정식으로부터
실근을 구하는 방법을 알고 있기 때문에 분석 사항에서 관계 식 부분을 이해할 수 있겠다. a, b, c가 사용자로부터
입력되기 때문에, a, b, c의 값에 따라서 실근을 구하는 방법을 생각해야 한다. |
||||||||||||||||||
| 설계 | |||||||||||||||||||
|
다음은 문제에 대한 최 상위 수준의 알고리즘이다.
위의 알고리즘에서 두 번째 단계가 사용자로부터 입력받은 a, b, c로부터 생성된 2차방정식으로부터 실근을 구하는 과정이다. 이 과정은 분석의 관계 식에서 기술된 사항으로부터 다음과 같이 다이어그램으로 나타낼 수 있다.
알고리즘 5-4-2에서 단계 2.6은 단순한 C 문장으로 번역되기에는 너무 복합한 수준이다. 이 단계는 다음과 같은 행동을 수행한다.
따라서 알고리즘 5-4-2의 단계 2.6을 다음과 같이 세분화시킨다. 위의 알고리즘의 각 단계는 단순한 C 문장으로 번역되기에 충분하다. 따라서 알고리즘의 세분화 과정은 여기서 멈춘다. |
|||||||||||||||||||
| 구현 | |||
|
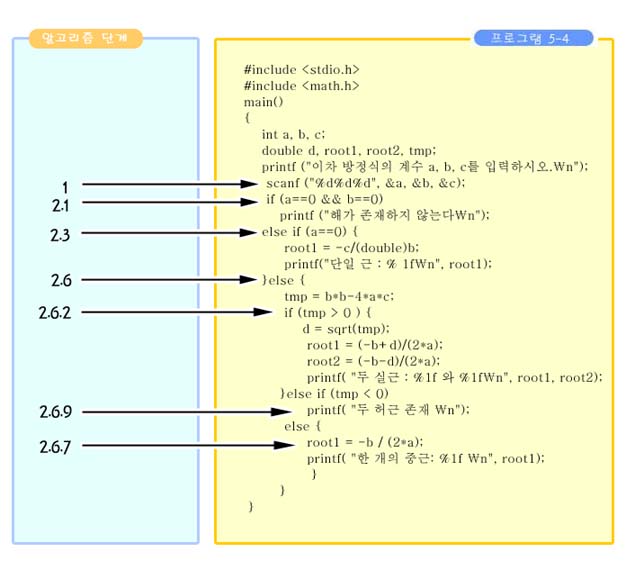
C는 제곱근을 수행할 수 있는 연산자를 제공하지 않는다. 그러나 제곱근을 수행하는 함수 sqrt()를 제공한다. 이 함수는 printf()처럼 미리 정의되어 있어서 필요하면 불러서 사용할 수 있다. 여러분이 printf()를 사용하기 위해서 이에 관한 정보를 포함하고 있는 표준 입출력 라이브러리 헤더 파일 <stdio.h>을 프로그램에 포함시켜왔음을 기억하라. 마찬가지로, sqrt() 함수를 사용하기 위해서 이에 관한 정보를 포함하고 있는 수학 라이브러리의 헤더 파일 <math.h>를 프로그램에 포함시켜야 한다. 수학 라이브러리는 수학에 관련된 유용한 여러 함수를 제공하고 있으며, 여러분은 필요하면 불러다 사용할 수 있다. 수학 라이브러리 사용에 관해서는 9주차 강의 2장에서 다룬다. 다음은 알고리즘 5-4-3에 대한 C 프로그램이다.
프로그램에서 다음 몇 가지 사항을 설명한다. 알고리즘 단계 2.4를 번역한 과정에서, b의 타입을 정수에서 double 타입으로 명시적으로 타입 변환을 수행하고 있다. 이것은 root1의 값이 double 타입의 값이기 때문이다. 만약, 명시적 타입 변환이 수행되지 않는다면, 소수점 이하 부분을 상실될 것이다. 단계 2.6.1을 번역한 과정에서, ( 단계 2.6.7과 2.6.9가 순서가 바뀌어져 있는데. 이것은 두 실수간의 동등성 비교를 가급적 피하기 위함이다. 물론, 여기서는 두 단계의 순서를 그대로 유지하여도 프로그램의 의미는 달라지지 않는다. |
|||
 |
다음
실습창을 통해서 프로그램
5-4를 실행시켜 본다. |



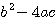 )의 제곱근을 취하기 전에 부호를 판단하고
있는데, 이것은 sqrt가 양의 값만을 취급하기 때문이다.
)의 제곱근을 취하기 전에 부호를 판단하고
있는데, 이것은 sqrt가 양의 값만을 취급하기 때문이다.


